2.1.3. ფუნქცია – PV საწყისი ღირებულების (დაბანდების) გამოანგარიშება

ფუნქციის ჩაწერის სინტაქსი ასეთია:

=PV(rate,nper,pmt,fv,type).

განვიხილოთ ფუნქციის გამოყენების ორი ვარიანტი.

ვარიანტი პირველი:

·        ანაზღაურება ხორციელდება თანხით სარგებლობის ვადის გასვლის შემდეგ. ამასთან, ყოველ პერიოდში არ ხდება ერთნაირი სიდიდის თანხის შეტანა – Pmt=0;

·        დარიცხვები ხორციელდება გარკვეული პერიოდულობით – Nper>0;

·        დარიცხვები ხორციელდება მუდმივი საპროცენტო განაკვეთით – Rate>0;

·        ანაზღაურება (დარიცხვა, დაბანდება) ხორციელდება პერიოდის ბოლოს – Type=0 ან პერიოდის დასაწყისში – Type=1;

·        სავარაუდო (დარიცხვების შემდეგ) მისაღები თანხის მნიშვნელობა ცნობილია –  FV>0;

saWiroa gamoviangariSoT sawyisi Tanxa.

PV, 1.1.-დან გამოიანგარიშება ფორმულით:

,                                                                       1.4

ამ შემთხვევაში ფუნქციის ჩაწერის სინტაქსი ასეთია:

 =PV(RATE,NPER,,FV,type).

ამოცანა

დავადგინოთ, რა თანხა უნდა იქნეს შეტანილი ბანკში ვადიან დეპოზიტზე, რომ ერთი წლის შემდეგ გვქონდეს 6000 ლარი, თუ ბანკი დაარიცხავს წელიწადში 13%-ს ყოველი თვის ბოლოს.

ამოხსნა

მოცემულია – სავარაუდო თანხა დეპოზიტის ვადის გასვლის შემდეგ –  FV= 6000 ლარი;

     წლიური საპროცენტო განაკვეთი – RATE = 13%;

     დარიცხვა ხორციელდება პერიოდის ბოლოს – Type=0;

     დეპოზიტის საერთო ვადა – ერთი წელი.

დარიცხვები ხორციელდება ყოველთვიურად, ე.ი. წელიწადში 12-ჯერ – NPER=12  1,08%-ით;.

ამ ამოცანისთვის PV ფუნქცია ასე ჩაიწერება:  =PV(13%/12,12,, 6000).

ამოხსნის შედეგად მივიღებთ, რომ საწყისი თანხა უნდა იყოს 5272 ლარი.

ვარიანტი მეორე:

·        ანაზღაურება ხორციელდება თანხით სარგებლობის ვადის გასვლის შემდეგ და ყოველ პერიოდში შეიტანება ერთნაირი სიდიდის თანხა – Pmt>0;

·        დარიცხვები ხორციელდება გარკვეული პერიოდულობით – Nper>0;

·        დარიცხვები ხორციელდება მუდმივი საპროცენტო განაკვეთით – Rate>0;

·        ანაზღაურება (დარიცხვა, დაბანდება) ხორციელდება პერიოდის ბოლოს – Type=0  ან პერიოდის დასაწყისში – Type=1;

·        სავარაუდო (დარიცხვების შემდეგ) მისაღები თანხის მნიშვნელობა ცნობილია – FV>0;

საჭიროა გამოვიანგარიშოთ საწყისი თანხა.

როცა Type=0, PV, 1.1-დან, გამოიანგარიშება ფორმულით,                                                   

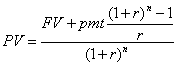                               1.5   

ამოცანა

საამშენებლო კომპანია ყიდის ბინას განვადებით 8 წლის განმავლობაში საფასურის სრულად დაფარვის პირობით. მყიდველმა ყოველწლიურად, წლის ბოლოს, კომპანიას უნდა გადაუხადოს 1500 ლარი, რომელიც შეიცავს ძირითად თანხას და წლიურ 8% სარგებელს.

დავადგინოთ, რას უდრის ბინის საწყისი ღირებულება; სულ რამდენი უნდა გადაიხადოს მყიდველმა ბინის საფასური და  რამდენი სარგებელი?

ამოხსნა

მოცემულია – პერიოდულად შესატანი თანხა Pmt=1500 ლარი;  

     წლიური საპროცენტო განაკვეთი – RATE = 8%;

     თანხის შეტანა ხორციელდება პერიოდის ბოლოს – Type=0;

      კომერციული ოპერაციის საერთო ვადა – რვა წელი.

ამ ამოცანისთვის PV ფუნქცია ასე ჩაიწერება:

=PV(8%,8,-1500,,1).

ამოხსნის შედეგად მივიღებთ, რომ ბინის საწყისი ღირებულება არის 9306 ლარი; სულ უნდა გადავიხადოთ  12000 ლარი, მათ შორის სარგებელი 2694 ლარი (12000-9306=2694).